Vektoren
Rechnen mit Vektoren im kartesischen Koordinatensystem
Es gibt außer der Addition und der Multiplikation mit einem Skalar weitere mathematische Operationen, die mit Vektoren möglich sind. Aus diesen Regeln ergeben sich häufig Vektorgleichungen, deren Lösung auf das Lösen von Linearen Gleichungssystemen hinausläuft.
Im Folgenden werden die Rechenregeln für Vektoren im dreidimensionalen kartesischen Koordinatensystem behandelt. Diese lassen sich prinzipiell auch auf mehr als drei Dimensionen erweitern.
Der Betrag eines Vektors
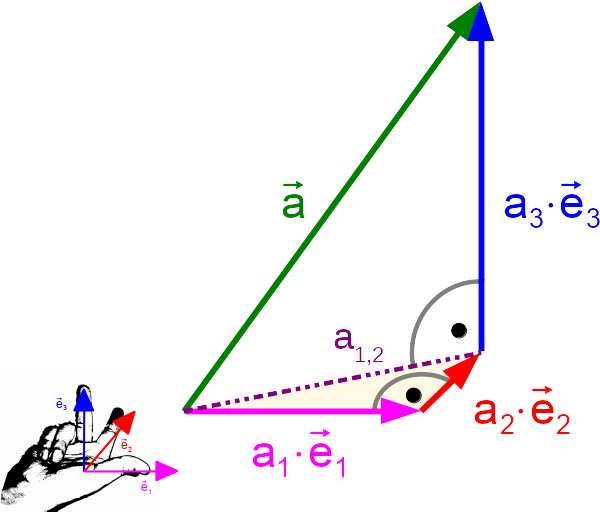
Länge (Betrag) eines Vektors im kartesischen Koordinatensystem
Geometrisch entspricht der Betrag eines Vektors seiner Länge. Diese lässt sich mit Hilfe des Satzes von Pythagoras auch in drei Dimensionen berechnen.
![]()
Linearkombinationen von Vektoren
Man kann einen Vektor a durch Aneinanderhängen von Vielfachen zweier oder mehrerer unterschiedlicher Vektoren bilden.
![]()
Man nennt dies eine Linearkombination von Vektoren.
Beispiel:

Eine Frage, die sich häufig stellt ist:
Wie kann ein bestimmter Vektor durch eine
Linearkombination aus vorgegebenen Vektoren gebildet
werden?
Beispiel:
Gegeben: 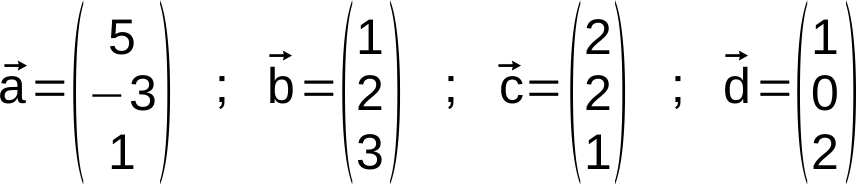
Gesucht: ![]()
Wie müssen die Faktoren k1, k2 und k3 lauten, damit die Vektorgleichung erfüllt ist?
Schreibt man die Vektorgleichung aus, so ergibt sich:
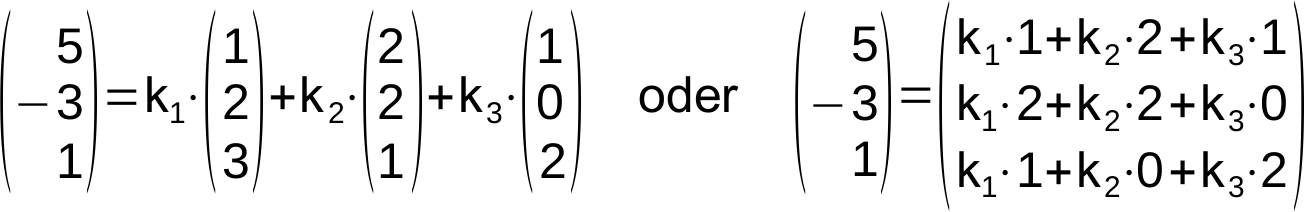
Es muss also ein Lineares Gleichungssystem gelöst werden.
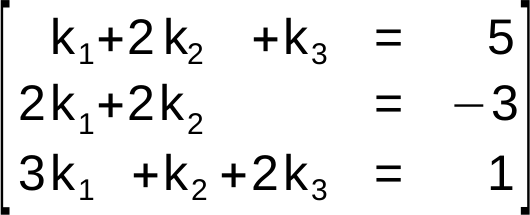
Die Lösung erhält man mit dem Gauß-Verfahren gelöst werden.
![]()
Lineare Unabhängigkeit von Vektoren
Vektoren heißen linear abhängig, wenn einer der Vektoren aus einer Linearkombination der anderen Vektoren hervorgeht.
Betrachten wir folgende Vektorgleichung:
![]() mit
mit ![]()
Gibt es für diese Gleichungen Lösungen k1,
k2 so bezeichnet man die Vektoren a, b und
c als linear
abhängig.
Man kann den Vektor a als
Linearkombination aus den Vektoren b und c
bilden.
Gibt es keine Lösung für diese Gleichung, so bezeichnet man die Vektoren a, b und c als linear unabhängig.
Geometrische Bedeutung der linearen Abhängigkeit von Vektoren
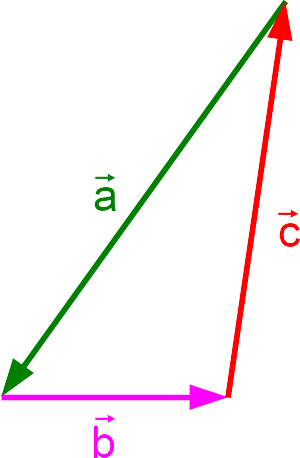
Geschlossener Vektorzug aus drei Vektoren
Sind drei (oder mehrere) Vektoren linear abhängig, kann man mit diesen Vektoren einen geschlossenen Vektorzug bilden.
Man kann also den Nullvektor als Linearkombination der drei Vektoren a, b und c bilden.
Die Gleichung
![]()
ist also lösbar so, dass mindestens zwei der Faktoren k1, k2 und k3 ungleich Null sind.
Anders gesagt: Ergibt die Gleichung
![]()
als einzige Lösung k1=k2=k3=0, müssen die Vektoren a, b und c linear unabhängig sein.
Die Lösung, bei der alle Faktoren gleich Null sind, bezeichnet man auch als Trivial-Lösung, da sie prinzipiell für alle Vektoren gilt.