Lineare Gleichungssysteme (LGS)
Was sind LGS?
Ein Lineares Gleichungssystem (LGS) besteht aus mehreren linearen Gleichungen mit mehreren Variablen. Die Gleichungen gehören zusammen und bilden eine System. Diese Zusammengehörigkeit wird oft auch grafisch (z.B. durch eckige Klammern) dargestellt.
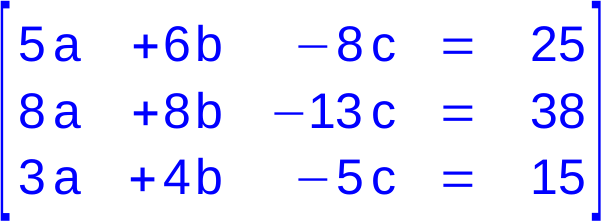
Beispiel für ein LGS mit drei Gleichungen und drei Variablen.
Lösungen von LGS
Gesucht sind die Werte der Variablen, für die alle Gleichungen (gleichzeitig) eine wahre Aussage ergeben.
Existieren Werte für die Variablen so, dass alle Gleichungen eine wahre Aussage ergeben, ist das LGS lösbar.
Die Wertekombinationen, für die Variablen werden dann als Lösungen bezeichnet.
Existiert nur eine mögliche Wertekombination als Lösung, so ist das LGS eindeutig lösbar.
Vereinfachte Darstellung von LGS
Um ein LGS einfacher und übersichtlicher darzustellen, kann man dieses in Matrix-Form schreiben.
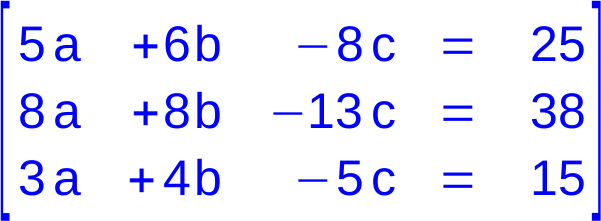
LGS in Gleichungs-Form |
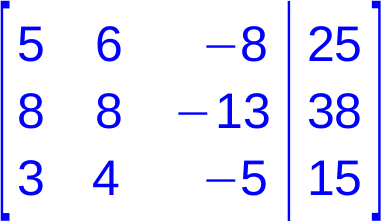
LGS in Matrix-Form als erweiterte Koeffizienten-Matrix |
In der Matrix werden nur die Vorfaktoren der Variablen (Koeffizienten) dargestellt. Das Gleichheits-Zeichen wird häufig durch eine senkrechte Linie symbolisiert.
Lösung mit dem Gauß-Verfahren
Das Gauß-Verfahren ist eine Methode zum Lösen von LGS, die auf Äquivalenzumformungen basiert.
Jede Gleichung (Zeile) eines LGS darf mit einer beliebigen Zahl ungleich Null multipliziert werden. Da es sich bei dieser Umformung um eine Äquivalenzumformung handelt, wird die Lösung der Gleichung nicht verändert.
Addiert man zwei Gleichungen eines LGS erhält man eine neue Gleichung. Ersetzt man eine der addierten Gleichungen durch die neu entstandene Gleichung, ändert man die Lösungsmenge des LGS nicht.
Das Gauß-Verfahren basiert auf einer Kombination aus Multiplikation und Addition von Gleichungen (wie oben beschrieben).
Beispiel für die Lösung eines LGS mit dem Gauß-Verfahren
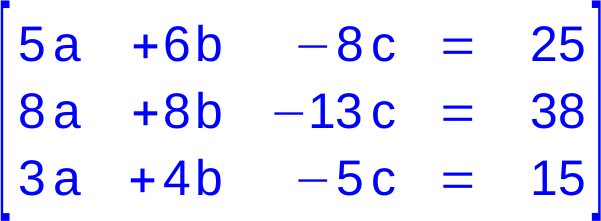
1. Umschreiben des LGS in Matrix-Form
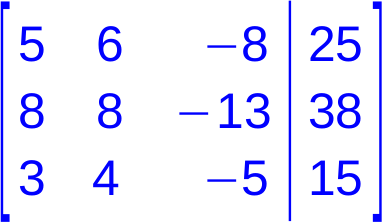
2. Auflösen der ersten Spalte
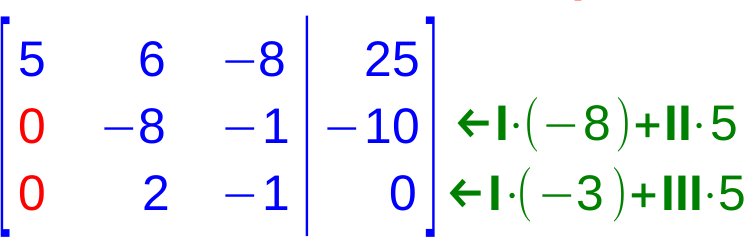
3. Auflösen der zweiten Spalte
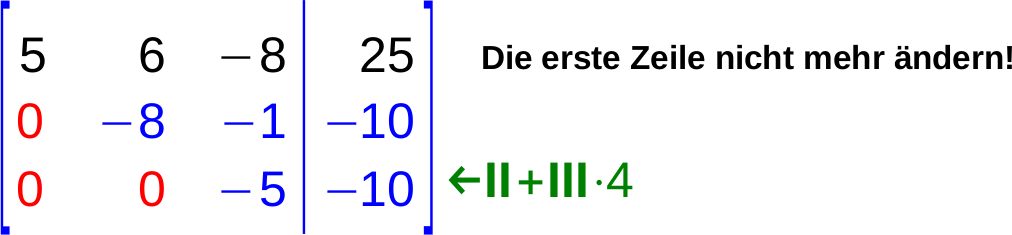
Stufen-Form
4. Die letzte Gleichung auflösen
![]()
5. In die nächste Gleichung einsetzen und auflösen
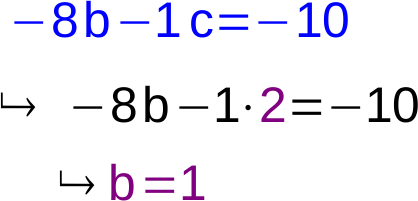
6. In die nächste Gleichung einsetzen und auflösen
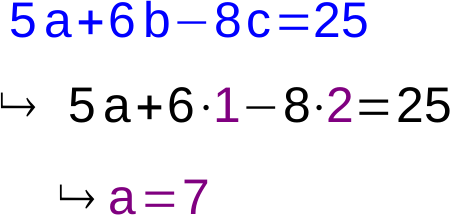
7. Lösung aufschreiben
![]()