Rechnen mit 1 und 0
Warum nur zwei Zustände?
Alle modernen Computer arbeiten intern mit nur zwei Zuständen. Diese werden durch zwei unterschiedliche Spannungen repräsentiert. Mit Halbleiterelementen (Transistoren) kann zwischen beiden Zuständen hin und hergeschaltet werden.
Theoretisch wären auch Prozessoren mit mehreren Spannungspegeln denkbar. Die elektronische Umsetzung wäre aber deutlich komplizierter. Ein solcher Prozessor wäre auch viel anfälliger auf elektromagnetische Störungen und damit unzuverlässiger als ein Prozessor, der nur zwei Zustände kennt.
Die beiden Zustände kann man durch die Spannungspegel High und Low definieren oder vereinfachend durch die Ziffern 1 und 0. Dies impliziert für mathematische Berechnungen die Verwendung des Dualsystems. Mit dem Dualsystem lassen sich alle mathematischen Operationen, die wir aus dem uns geläufigen Dezimalsystem kennen, genauso durchführen.
Allerdings müssen die mathematischen Rechenregeln auch auf geeignete Weise in elektronische Schaltungen übersetzt werden. Erst dann kann der Computer Berechnungen auch durchführen.
Boolesche Algebra
Die mathematisch formale Grundlage für die Umsetzung von Mathematik in Elektronik ist die Boolesche Algebra.
Die Boolesche Algebra ist ein Teilgebiet der Mathematik, das sich mit der Aussagenlogik befasst. Benannt ist sie nach
George Boole (1815-1864), der als Begründer der modernen, formalisierten mathematischen Logik gilt.
Die Boolesche Algebra kennt als Grundmenge nur zwei Zustände, nämlich wahr oder falsch. Vereinfachend werden diese Zustände durch die Ziffern 1 und 0 repräsentiert, wobei 1 für wahr und 0 für falsch steht.
Die Boolesche Algebra basiert also auf der Grundmenge {0,1}, auf welcher drei logische Operationen (logische Grundfunktionen) definiert sind. Die logischen Grundfunktionen UND, ODER, NICHT lassen sich schaltungstechnisch einfach umsetzen. Man spricht dann von der Schaltalgebra.
Die UND-Funktion
Die UND-Funktion wird auch als Konjunktion bezeichnet. Sie ist eine Verknüpfung mit (mindestens) zwei Eingängen und einem Ausgang (Ergebnis). Das Ergebnis einer UND-Funktion ist wahr, wenn beide (alle) Eingänge wahr sind. Die UND-Funktion wird mit dem Symbol ⋀ abgekürzt. Manchmal wird statt ⋀ auch das Symbol für die Multiplikation ⋅ verwendet.
Sind A und B die Eingänge einer UND-Funktion und Y der Ausgang, so kann man die UND-Funktion symbolisch als booleschen Term darstellen. In der Schaltalgebra werden boolesche Terme als Schaltfunktionen bezeichnet.
Eine andere Möglichkeit der Darstellung einer logischen Funktion ist die Wahrheitstabelle.

Die ODER-Funktion
Die ODER-Funktion wird auch als Disjunktion bezeichnet. Sie ist eine Verknüpfung mit (mindestens) zwei Eingängen und einem Ausgang. Das Ergebnis einer ODER-Funktion ist wahr, wenn mindestens einer der Eingänge wahr ist. Die ODER-Funktion wird mit dem Symbol ⋁ abgekürzt. Manchmal wird statt ⋁ auch das Symbol für die Addition + verwendet.

Die NICHT-Funktion
Die NICHT-Funktion wird auch als Negation bezeichnet. Sie ist eine Verknüpfung mit einem Eingang und einem Ausgang. Das Ergebnis einer NICHT-Funktion ist wahr, wenn der Eingang falsch ist. Das Ergebnis einer NICHT-Funktion ist falsch, wenn der Eingang wahr ist. Die NICHT-Funktion wird mit dem Symbol ¬ abgekürzt. Häufig wird die NICHT-Funktion auch durch Überstreichen der negierten Variablen gekennzeichnet.
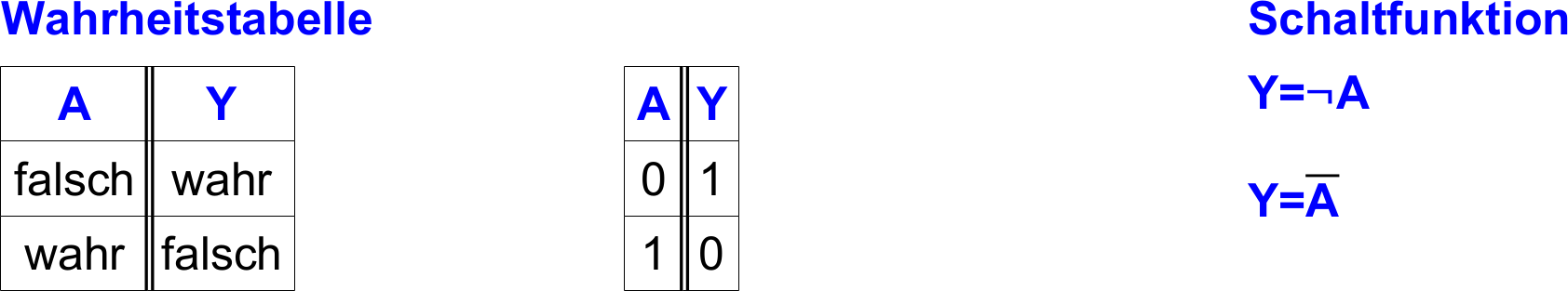
In elektronischen Schaltungen wird die Negation auch als Invertierung bezeichnet. In der Mathematik hat jedoch der Begriff invers bzw. inverses Element eine andere Bedeutung als in der Schaltalgebra.
Die Grundrechenarten
Nun geht es darum, wie man die Grundrechenarten mit Hilfe der Booleschen Algebra realisieren kann. Da alle Grundrechenarten auf der Addition basieren, muss als Erstes auch ein Weg gefunden werden, die Addition mit Hilfe einer geeigneten Kombination der drei logischen Grundgatter zu realisieren.
Die Addition von Dualzahlen
Im Prinzip funktioniert die Addition von Dualzahlen genauso wie die Addition von Dezimalzahlen. Durch den begrenzten Ziffernvorrat kommt es jedoch viel häufiger zu einem Übertrag.
Beispiel: Addition zweier Dualzahlen

Der begrenzte Ziffernvorrat bringt jedoch auch wichtige Vorteile, die bei der elektronischen Umsetzung hilfreich sind. Prinzipiell werden bei der Addition die Stellen gleicher Wertigkeit addiert, der Übertrag wird dann zur den Stellen der nächsthöheren Wertigkeit addiert. Bei der Addition zweier Zahlen ergibt sich so eine begrenzte Zahl an Möglichkeiten. Es geht letztendlich darum Zwei Zahlen und ggf, einen Übertrag (also drei Dualzahlen) zu Addieren. Das Ergebnis dieser Addition besteht aus einer Zahl und einem Übertrag (also aus zwei Dualzahlen).
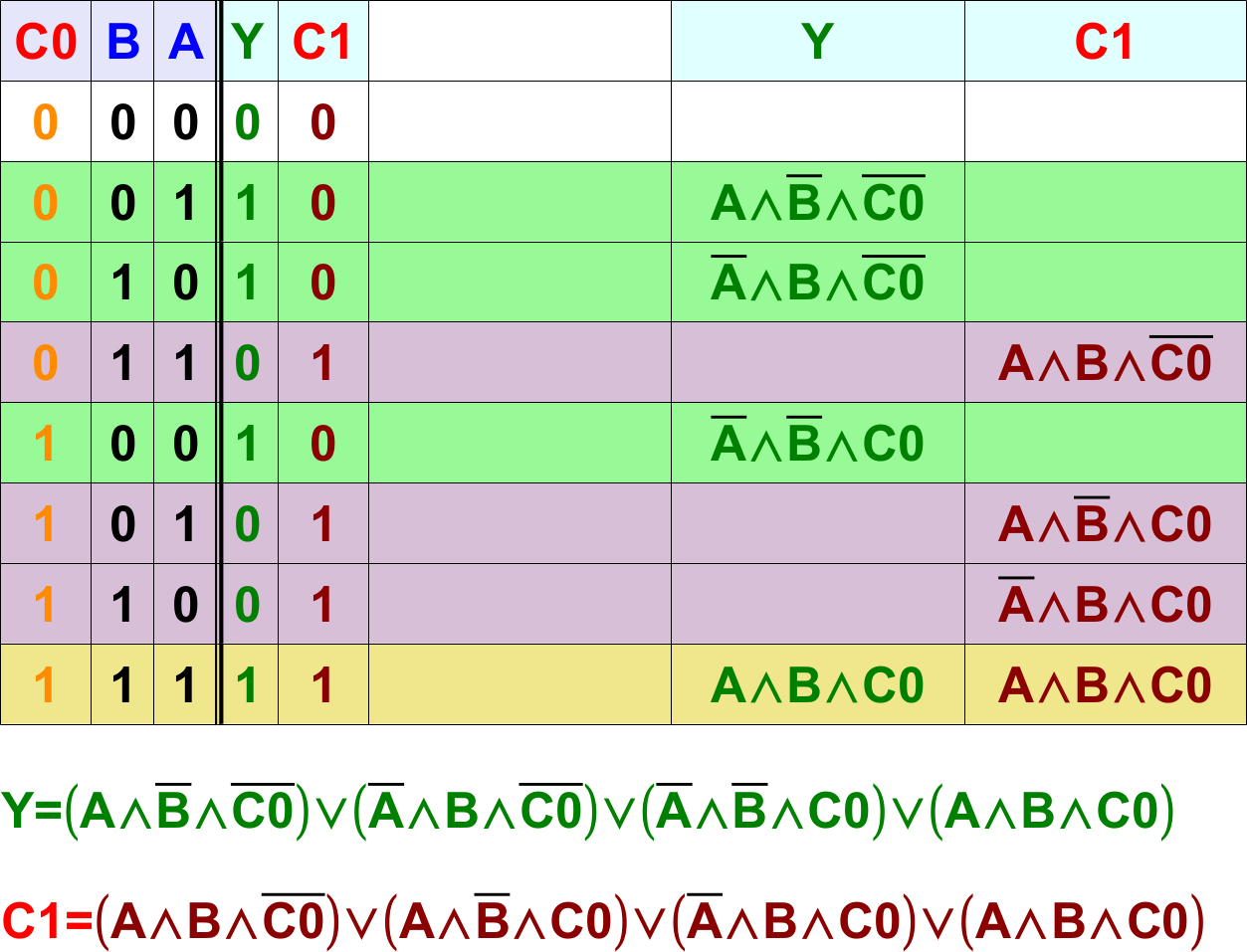
Wahrheitstabelle für die Addition dreier Dualzahlen mit Übertrag:

Sollen zwei Dualzahlen addiert werden, gilt für jede Stelle die obige Wahrheitstabelle. Auf diese Weise können beliebige Dualzahlen addiert werden.
Der Volladdierer
Die oben angegebene Wahrheitstabelle kann man mit Hilfe logischer Grundgatter realisieren. Man erhält dann einen "Bauplan" für einen Volladdierer. Durch Kaskadierung (Wiederholung) solcher Volladdierer können mehrstellige Dualzahlen addiert werden.
Realisierung eines Volladdierers mit logischen Grundgattern:
Dies ist nur eine Möglichkeit einen Volladdierer aus logischen Grundgattern aufzubauen. Durch Optimierung kann die Schaltfunktion noch vereinfacht werden, was bei der Umsetzung elektronische Bauteile einspart.
der Halbaddierer
Der Halbaddierer (HA) ist ein Baustein, der in digitalen Schaltungen häufig zu finden ist. Ein Halbaddierer addiert zwei einstellige Dualzahlen zu einem einstelligen Ergebnis mit Übertrag.
Die Wahrheitstabelle eines Halbaddierers entspricht ersten vier Zeilen der Wahrheitstabelle eines Volladdierers (C0=0).
