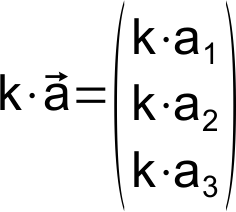Vektoren
Rechnen mit Vektoren
Um mit Vektoren "rechnen" zu können, benötigt man die algebraische Darstellung von Vektoren.
Doch wie gelangt man von der geometrischen Darstellung eines Vektors (als Pfeil im Raum) zur algebraischen Darstellung als Zahlen-Tupel?
Dazu muss man zunächst definieren für was die Komponenten eines Vektors überhaupt stehen.
Das Bezugssystem
Die Komponenten eines Vektors sind eng mit dem Bezugssystem des Vektors verbunden.
Das Bezugssystem (auch Koordinatensystem) besteht aus mehreren Einheitsvektoren, die nicht paarweise zueinander parallel sein dürfen. Diese Einheitsvektoren (auch Basisvektoren oder Basis genannt) spannen den gesamten Vektorraum über dem Bezugssystem auf.
Die Dimension eines Vektorraums ist gleich der Anzahl der Basisvektoren, die benötigt wird, um den gesamten Vektorraum aufzuspannen.
Beispielsweise wird der uns wohlbekannte dreidimensionale Raum von genau drei Basisvektoren vollständig aufgespannt.
Die Vektoren, die die Basis des Vektorraums bilden, also das Bezugssystem oder Koordinatensystem des Vektorraums, müssen nicht zwangsweise gleich lang sein und auch nicht unbedingt senkrecht aufeinander stehen.
Außerdem existieren unendlich viele unterschiedliche Bezugssysteme, die einen Vektorraum aufspannen.
Die Komponenten eines Vektors ändern sich normalerweise, wenn man unterschiedliche Bezugssysteme wählt (Koordinatentransformation).
Das kartesische Koordinatensystem
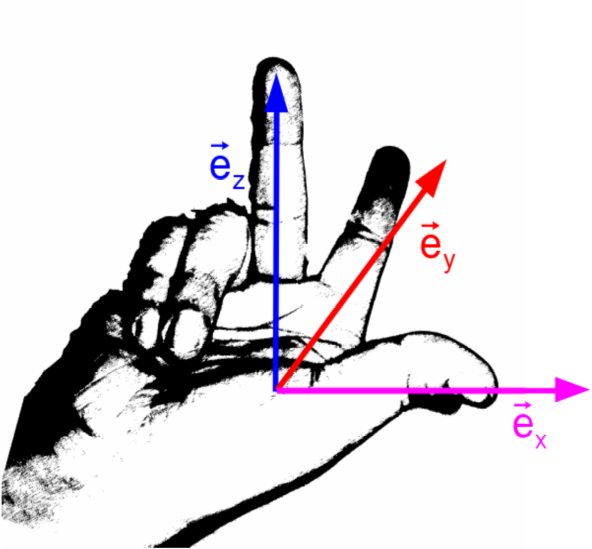
Rechtssystem
Das uns geläufigste Bezugssystem ist das kartesische Koordinatensystem.
Es ist ein Orthonormalsystem, dessen Basisvektoren ein Rechtssystem bilden (siehe Abbildung rechts).
Die Basisvektoren besitzen die selbe Länge und stehen paarweise senkrecht aufeinander.
Die Basisvektoren eines kartesischen Koordinatensystems werden meistens mit ex, ey und ez (manchmal auch mit e1, e2, e3) bezeichnet.
Von der geometrischen zur algebraischen Darstellung
Ein Vektor wird geometrisch durch einen Pfeil im Raum dargestellt. Er repräsentiert quasi den direkten Weg vom Anfang bis zum Ende (Pfeilspitze) des Vektors.
Man kann diesen Weg aber auch abschnittsweise zurücklegen, indem man sich zunächst in x-Richtung, dann in y-Richtung und dann in z-Richtung bewegt.
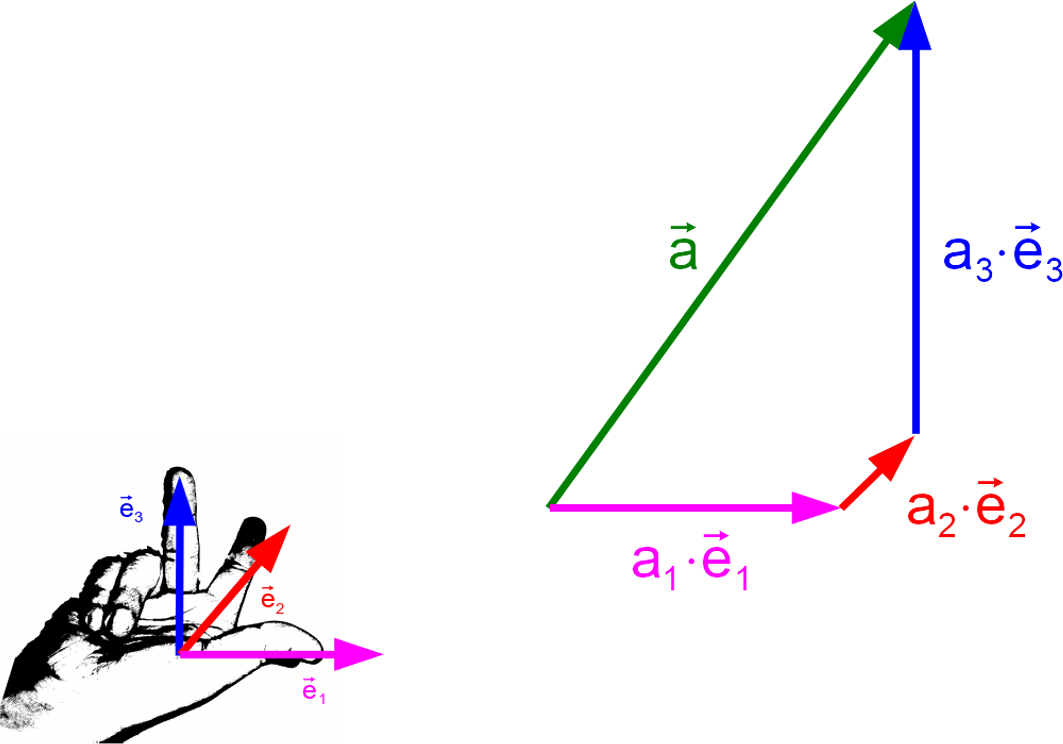
Zerlegung eines Vektors in seine Komponenten
Jeder beliebige Vektor im dreidimensionalen Raum kann also durch die Addition von Vielfachen der Basisvektoren auf eindeutige Weise gebildet werden. Die Faktoren, mit denen man die Basisvektoren multiplizieren muss, sind die Komponenten des Vektors.
![]() sind Basisvektoren des Vektorraums
sind Basisvektoren des Vektorraums
Algebraische Darstellung: 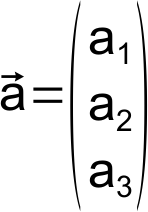
Diese Bildungsvorschrift gilt allgemein für n-dimensionale Vektorräume und für beliebige Bezugssysteme.
Rechenregeln für Vektoren
Wir können nun die Rechenregeln für die Addition und Multiplikation von Vektoren in algebraischer Form definieren.
Addition
Geometrisch entspricht die Addition zweier Vektoren dem Aneinanderhängen dieser Vektoren. Algebraisch entspricht die Addition der Addition der Komponenten der Vektoren, was aus der obigen Herleitung direkt hervorgeht.
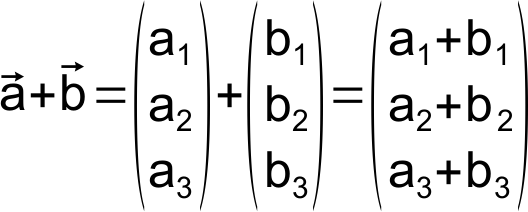
Multiplikation mit einem Skalar
Geometrisch entspricht die Multiplikation eines Vektors mit einem Skalar der Verlängerung bzw. Verkürzung des Vektors. Algebraisch müssen alle Komponenten des Vektors mit dem Skalar multipliziert werden.